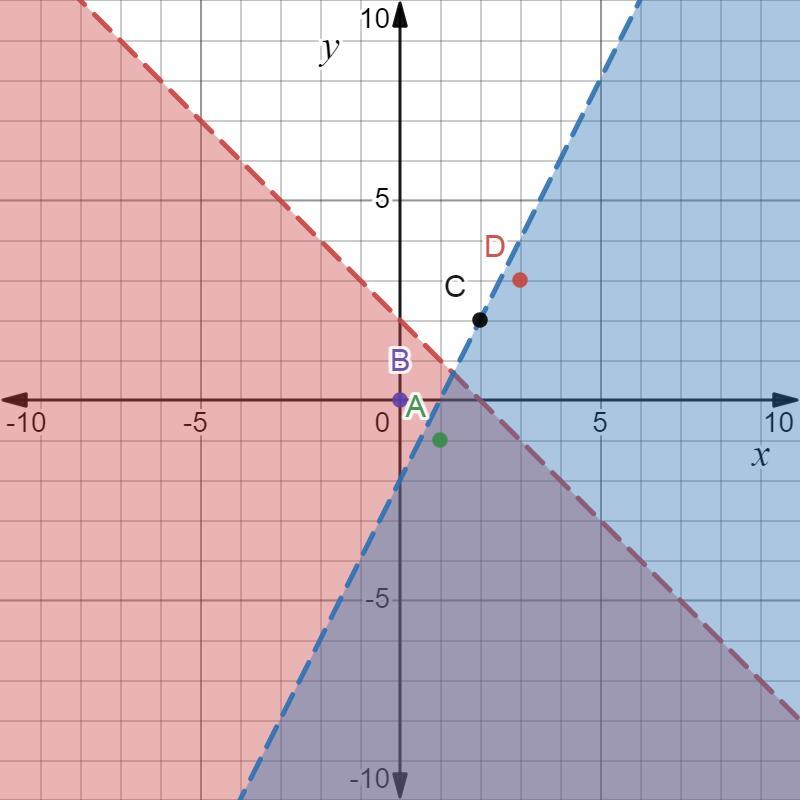
5.) Which point satisfies the following system
of inequalities?

y=-x+2
-2x+y<-2
Á.(1,-1) B.(0,0) C. (2,2) D.(3,3)

The three-period weighted moving average forecast for period 5 is option (B) 146.4.

In forecasting, the weighted moving average method is commonly used to estimate future values by giving more weight to the recent observations than the older ones.

To calculate the three-period weighted moving average, we need to apply the given weights of 0.5, 0.3, and 0.2 to the last three periods' data. The formula for calculating the weighted moving average is:

Weighted Moving Average = (w₁Y₁) + (w₂Y₂) + (w₃*Y₃)

where w₁, w₂, and w₃ are the weights assigned to the most recent period, second most recent period, and third most recent period, respectively. Y₁, Y₂, and Y₃ are the corresponding values of the periods.

Applying this formula to the given data, we get:

Weighted Moving Average = (0.5148) + (0.3144) + (0.2*146)

= 74 + 43.2 + 29.2

= 146.4

Therefore, the correct option is (B).

To know more about average here.

https://brainly.com/question/16956746

#SPJ4

Answer:

b

Step-by-step explanation:to get the answer you multiply by 4 1x4 =4 3 x 4=12

The value of x in the domain of function f(x) = √(x - 11) will be 13. Then the correct option is A.

A function is an assertion, concept, or principle that establishes an association between two variables. Functions may be found throughout mathematics and are essential for the development of significant links.

The domain means all the possible values of x and the range means all the possible values of y.

The function is given below.

f(x) = √(x - 11)

The value inside the square root should be greater than or equal to zero. Then we have

x - 11 ≥ 0

x ≥ 11

The value of x in the domain of function f(x) = √(x - 11) will be 13. Then the correct option is A.

More about the function link is given below.

https://brainly.com/question/5245372

#SPJ9

The correct values of a and b, expressed in their simplest form is a = 7 and b = 97/23

An equation is a statement that shows the equality between two expressions. It contains an equal sign (=) and two sides that represent the same value.

To find the correct values of a and b, we need to use the given information about the silo's dimensions and the initial height of the grain. The radius of the silo is 10 meters and the height is 100 meters. The grain is initially at a height of 7 meters, so the remaining height that needs to be filled is

=> 100 - 7 = 93 meters.

Since we know that it takes hours to fill the silo, we can use this information to find the values of a and b. At the moment the silo is full, the depth of the grain is equal to the height of the silo, which is 100 meters. We can use this to form an equation:

d( ) = a³ + b = 100

We know that the total depth of the grain is the sum of the initial depth of 7 meters and the cubic equation that models the additional depth of the grain as more is poured into the silo. So we have:

d(t) = 7 + at³ + b

Now we can substitute this expression into the previous equation and solve for a and b:

7 + a³ + b = 100

a³ + b = 93

We have two unknowns, a and b, so we need another equation to solve for them. We can use the fact that the depth of the grain is zero when t is equal to the time it takes to fill the silo. This means that:

d( ) = 0 = 7 + a³ + b

Now we have two equations:

a³ + b = 93

a³ + b = -7

We can subtract the second equation from the first to eliminate b:

0 = 100

This is a contradiction, which means that there is no solution for a and b that satisfies the given conditions. Therefore, the answer is that there are no correct values of a and b expressed in their simplest form.

To know more about equation here.

https://brainly.com/question/10413253

#SPJ4

Type 1 error is rejecting the null hypothesis, even when we know it is true. Here the average diameter is 1.65mm, but we decide that it is not 1.65mm.

The data which given says that the average diameter should be 1.65mm. Bigger and smaller diameters may result in problems like pain and rupture of RBCs.

So the null and alternate hypothesis are

Null hypothesis , H₀ : μ= 1.65 mm

Alternate hypothesis, H₁ : μ≠ 1.65 mm

Here the sample size, n= 35, σ = 0.07, mean = 1.64

Type 1 error means rejecting null hypothesis, when it is true. It is also known as false positive error. A false positive can occur if something other than the stimuli applied during the test is resulting the outcome. This cannot be avoided because of the degree of uncertainty involved.

In type 1 error, we assume that the null hypothesis, H₀ : μ=1.65 is false, that means the average diameter is not 1.65 mm, even if the actual diameter is 1.65 mm.

Se decide average diameter is not 1.65 mm.

For more information regarding errors in statistical analysis, kindly refer

https://brainly.com/question/29893319

#SPJ4

The correct option regarding the number of x-intercepts of each function is given as follows:

Both functions have the same number of x-intercepts.

The x-intercept of a function is given by the value of x when f(x) = 0, that is, the value of x when the function crosses the x-axis.

From the Table, for function A, these values are given as follows:

x = 1 and x = 3.

For Function B, the intercepts are given as follows:

|x| - 2 = 0

|x| = 2

x = -2 or x = 2.

The intercepts are different, but both functions have the same number of x-intercepts.

More can be learned about functions at https://brainly.com/question/24808124

#SPJ1

Answer:

Both functions have the same number of x-intercepts.

Step-by-step explanation: Did the test, got it correct.

The probability that each bill is a $1 bill is given as follows:

1/16.

A probability is calculated as the division of the desired number of outcomes by the total number of outcomes.

The bills are replaced, hence we consider that for each trial, there is a 1/4 probability of selecting a $1 bill, as one out of the four bills are of $1.

Hence the probability that each bill is a $1 bill is obtained as follows:

p = 1/4 x 1/4

p = 1/16.

More can be learned about probability at https://brainly.com/question/24756209

#SPJ1

Answer:

Step-by-step explanation:

To find 53 using the equation vw=(2vw)^2 - (v+w)^3, we need to substitute v=5 and w=3 into the equation:

5~3 = (2(5)(3))^2 - (5+3)^3

Simplifying:

5~3 = (30)^2 - (8)^3

5~3 = 900 - 512

5~3 = 388

Therefore, 5~3 is equal to 388.

The evaluation of F(-2) is 18 and the value of x when f(x)=1 is 1/8.

There are many tools we can use to find the information of the relation which was used to form the graph.

A graph contains data of which input maps to which output.

Analysis of this leads to the relations which were used to make it.

For example, if the graph of a function is rising upwards after a certain value of x, then the function must be having increasingly output for inputs greater than that value of x.

If we know that the function crosses x axis at some point, then for some polynomial functions, we have those as roots of the polynomial.

Given that;

f(x)= -8x + 2

Now substituting -2 in f(x) to find the value of f(-2)

f(-2)=-8*-2+2

f(-2)=16+2

f(-2)=18

If the value of f(x)=1

1=-8x + 2

-1=-8x

x=1/8

Therefore, the value of function  f(-2) and when f(x) is equal to -1 will be 18 and 1/8

Learn more about finding the graphed function here:

https://brainly.com/question/27330212

#SPJ9

[tex]\textit{Pythagorean Identities} \\\\ \sin^2(\theta)+\cos^2(\theta)=1\implies \sin^2(\theta)=1-\cos^2(\theta)\\\\\\ 1+\cot^2(\theta)=\csc^2(\theta) \\\\[-0.35em] ~\dotfill\\\\ \boxed{1+cot^2(x)}-cos^2(x)-cos^2(x)cot^2(x) \\\\\\ \boxed{csc^2(x)}-cos^2(x)-cos^2(x)cot^2(x)\implies csc^2(x)-cos^2(x)[1+cot^2(x)] \\\\\\ csc^2(x)-cos^2(x)[csc^2(x)]\implies csc^2(x)[1-cos^2(x)]\implies csc^2(x)sin^2(x) \\\\\\ \cfrac{1}{sin^2(x)}\cdot sin^2(x)\implies \text{\LARGE 1}[/tex]

The Population parameter is population mean i.e μ. The Interpretation of 90% confidence that population mean i.e μ lies between 116.8 and 149.2.

We have, a Normalised average amount of time, in minutes, data for students to complete a standardized test.

Sample size, n = 49

Significance level, = 90% = 0.90

Confidence interval is range of values. It is calculated by below formula, confidence interval,

CI = Mean ± Z( standard deviations/sample size)

but we have, the 90% confidence interval is equals to [116.8,149.2]. The population is a large set and it is deficult to work on population, so sample subsets of it are considered for observation. Population parameter is population mean. The interpretation from provide informations about 90% of confidence interval is that population mean lie between 116.8 and 149.2, i.e., 116.8 ≤ μ ≤149.2.

To learn more about Confidence interval, refer:

https://brainly.com/question/17212516

#SPJ4

The rounded numbers for the given decimal numbers are 4, 8 and 9.

To change a number into an approximation having fewer significant digits, is called the rounding numbers.

For example :- Round off 15.4 to 15, round off 15.51 to 15.5 or to 16, round off 0.499 to 0, and round off 970,000 to 1 million.

Given are three decimal numbers, 3.896, 7.8143 and 9.3959 we are asked to round them to whole number.

The rule for rounding the numbers is :-

Example: 38 rounded to the nearest ten is 40.

Example: 33 rounded to the nearest ten is 30.

Therefore, in 3.896, the number after the decimal is 8 which is greater than 5 so rounding up we will get, 4

Similarly, 7.8143 = 8

And in 9.3959, the number after the decimal is 3 which is smaller than 5 so rounding down we will get, 9

Hence, the rounded numbers for the given decimal numbers are 4, 8 and 9.

Learn more about rounding numbers, click;

https://brainly.com/question/5536190

#SPJ9

The complete table is shown in the picture attached. The sale price of the product is $24.

The sale price is the original price minus the discount. It can be expressed as

S = P - D

Where

The discount when an item is on sale can be calculated by

D = d × P

Where d = percent of discount.

Complete the table shown in the picture!

We have

To complete the table, we should find the sale price.

From the information, the discount is

D = d × P

D = 80% × $120

D = $96

The sale price will be

S = P - D

S = $120 - $96

S = $24

The product has a sale price of $24.

The second picture attached shows the complete table.

Learn more about percentage here:

brainly.com/question/29832925

#SPJ1

The area of the trapezium will be 168 ft².

What is a trapezium, exactly?

Trapezoids have two parallel sides and two oblique sides. Another term for it is a trapezium. A trapezoid is a four-sided closed form with a space-filling perimeter. It is a 2D figurine, not a 3D figure. The bases of a trapezoid are parallel to one another. Legs are non-parallel sides, sometimes referred to as lateral sides and height is the distance between the parallel sides.

The area of a trapezium is equal to 1/2*(a+b)*h.

where h is the distance or height between two parallel lines

Lines a and b are parallel.

Now,

As we can decompose given trapezium into a rectangle with length=18 ft and breadth=8 ft and a triangle with base=6 ft and height=8 ft.

Then area of trapezoid=area of rectangle + area of triangle

=l*b+1/2*b*h

=18*8+1/2*6*8

=144+24

=168 ft²

Hence,

           The area of the trapezium will be 168 ft².

To know more about Trapeziums visit the link

https://brainly.com/question/12003076?referrer=searchResults

#SPJ1

Answer:

The only score that falls outside of this range is 35, so that is the outlier.

Step-by-step explanation:

To find the mean of Allins test scores, we add up all the scores and divide by the number of scores:

Mean = (88+90+35+92+82+90)/6 = 77.83 (rounded to two decimal places)

To find the median, we need to arrange the scores in order from least to greatest:

35, 82, 88, 90, 90, 92

The median is the middle value, which in this case is 89.

To find the mode, we look for the value that appears most frequently. In this case, the mode is 90, since it appears twice.

To find the range, we subtract the lowest score from the highest score:

Range = 92 - 35 = 57

To identify the outlier in the data set, we can use the interquartile range (IQR) and the rule that any data point more than 1.5 times the IQR below the first quartile or above the third quartile is considered an outlier.

First, we need to find the quartiles:

Q1 (first quartile) = 80 (the median of the lower half of the data set)

Q3 (third quartile) = 91 (the median of the upper half of the data set)

IQR = Q3 - Q1 = 11

Any data point more than 1.5 times the IQR below Q1 or above Q3 is considered an outlier.

Lower outlier threshold = Q1 - 1.5(IQR) = 63.5

Upper outlier threshold = Q3 + 1.5(IQR) = 107.5

The only score that falls outside of this range is 35, so that is the outlier.

Answer:

  x = 1

Step-by-step explanation:

You want the solution to the equation √(x²+2x+6) +x² = √(2x+2) -x +3.

We find a graphing calculator to be a useful tool for finding the solutions to equations like this. It shows the solution to be x = 1.

Solved in the usual way, this would resolve to an 8th degree equation with one integer factor: (x -1). The remaining 7th degree polynomial factor has 3 real roots and 4 complex roots. All of these 7 irrational solutions are extraneous. (They do not satisfy the original equation.)

The solution is x = 1.

__

Additional comment

Our approach to removing the radicals is to ...

The usual approach to looking for roots is to use Descartes' rule of signs and the Rational Root theorem.

You can determine there are 3 or 1 positive real roots, and 5, 3, or 1 negative real roots. The only rational real roots will be ±1 or ±47, and we know that ±47 can't work. (47^8 will not be balanced by any of the other terms in the polynomial.)

You can see already that the graphing calculator approach is much preferred.

<95141404393>

When a research is conducted on a randomly chosen representative sample, hypothesis testing involves gathering data and calculating how likely a specific set of data is. No connection exists between the factors.

The t test is the most used null test for this statistical connection. Only one t test, the reliant t test, as well as the individual t test are three different t test types that are examined in this section and are used to a variety of study methods.

The probability that you would have discovered a certain collection of data if the null hypothesis had been correct is expressed as a number called the p value, which is determined from a statistical test. In order to determine either to reject a null hypothesis, P values are utilized in hypothesis testing.

To know more about Hypothesis testing visit:

https://brainly.com/question/30588452

#SPJ1

The larger number is 16 and the smaller number is -15.

The numbers are obtained by a system of equations, for which the variables are given as follows:

x and y.

The sum of two numbers is 1, hence:

x + y = 1.

y = 1 - x.

Three times the larger number plus two times the smaller number is 18, hence:

3x + 2y = 18.

Replacing the first equation into the second, the value of x is obtained as follows:

3x + 2(1 - x) = 18

3x + 2 - 2x = 18

x = 16.

Then the value of y is of:

y = 1 - x

y = 1 - 16

y = -15.

More can be learned about a system of equations at https://brainly.com/question/30630891

#SPJ1

Answer:

Step-by-step explanation:

since y = -8x + 6

if x=-10, y=-8x10+6=-74, so A is not the solution

if x =-8, y=-8x(-8)+6=70, so B is not the solution

if x =5, y=-8x5+6=-34, so C is the solution

if x =3, y=-8x3+6=-18, so D is not the solution

He had 48.75 oz of salsa.

In mathematics, multiplication is a method of finding the product of two or more numbers. It is one of the basic arithmetic operations, that we use in everyday life.

here, we have,

I guess that Clay is filling 6.5 oz bottles of salsa.

And we know that he was able to fill 7.5 of these bottles,

then if each bottle has 6.5 oz, 7.5 of them have a total mass of salsa will be equal to 7.5 times 6.5 ounces,

this is:

M = 7.5*6.5 oz = 48.75 oz

This means that Clay had 48.75 ounces of Salsa

A drawn model to show this is seen below.

Each big square represents 0.5 oz,

and the area black delimited area represents a total amount of 6.5 oz, we have 7 of them, then you can draw that 7 times,

and count the squares,

and then you will find the total ounces of salsa that Clay had, which is equivalent to the multiplication we did above.

To learn more on multiplication click:

brainly.com/question/5992872

#SPJ9

The simplification of the given expression

[tex]5 \sqrt[3]{250} - 3 \sqrt[3]{686} [/tex]

is

[tex] = 4 \sqrt{2} [/tex]

[tex]5 \sqrt[3]{250} - 3 \sqrt[3]{686} [/tex]

[tex] = 5 \sqrt[3]{125 \times 2} - 3 \sqrt[3]{343 \times 2} [/tex]

[tex] = 5 \times 5 \sqrt{2} - 3 \times 7 \sqrt{2} [/tex]

[tex] = 25 \sqrt{2} - 21 \sqrt{2} [/tex]

[tex] = 4 \sqrt{2} [/tex]

Consequently,

[tex]4 \sqrt{2} [/tex]

is the answer to the given expression.

Read more on simplification of expression:

https://brainly.com/question/723406

#SPJ1

(a) The distribution of T is Geometric Distribution and parameter is p which ranges from 0 to 1.

(b) p(x - a) - p[tex](1-p)^{a-1}[/tex] where, x is probability that the xth trial is the first success [tex]$\hat{A} \hat{A} P[/tex] is the probability of success.

(c) Expected pay-off retains are negative, so this is an unfair game.

The probabilities of winning $1 million are [tex]$P_1$[/tex] and [tex]$P_2$[/tex] respectively.

(a) Let 'T ' be the number of times you play until winning at least one prize.

T follows Geometric Distribution, it has only parameter P which is the probability of success which ranges between 0 and 1.

(b) Its probability density function is.

p(x - a) - p[tex](1-p)^{a-1}[/tex]

where, x is probability that the xth trial is the first success [tex]$\hat{A} \hat{A} P[/tex] is the probability of success.

Expected payoff: pw - (1 - p) x dollar

Where:-

p is the probability of success

[tex]$\omega$[/tex] is the lottery winning amount

[tex]$\alpha$[/tex] is the lottery buying cost

(c) [tex]$P=\frac{1}{292,201,338} & =0.0000000034 \\[/tex]

Expected payoff = [tex]p \times 1,000,000-(1-p) 10 \\[/tex]

= 0.0034 - 9.999999966 \\

= -9.99659966

Expected pay-off retains are negative, so this is an unfair game.

[tex]$p=\frac{1}{3,02,575,350} & =0.0000000033 \\[/tex]

Expected pay-off  [tex]& =p \times 10000000-(1-p) 10 \\[/tex]

= 0.0033 - 9.999999967

= -9.996699967

Winning probability [tex]( $P_s$ )[/tex] are so low that expected returns are negative.

For more questions on probability

https://brainly.com/question/7579947

#SPJ4

The set of all points on the real line whose distance from zero is less than 8 can be described by the absolute value inequality:

|x| < 8

where |x| denotes the absolute value of x. This inequality can be read as "the distance between x and 0 is less than 8".

Geometrically, this inequality describes the open interval (-8, 8) on the real number line, which includes all real numbers that are between -8 and 8 but not including -8 and 8 themselves. In other words, the set of all points on the real line that are within 8 units of the origin, excluding the origin itself.

For more such questions on Inequality

https://brainly.com/question/25944814

#SPJ4

As a result, V is a vector space over the real number field.

As per the question given,

Yes, V is a vector space over the field of real numbers with the given operations.

To show this, we need to verify that the following vector space axioms are satisfied for any vectors u, v, and w in V and any scalars a and b in F:

All of these axioms are easily verified using the given operations. Therefore, V is a vector space over the field of real numbers.

For such more questions on Vector Space

https://brainly.com/question/11383

#SPJ4

The volume of the rectangular tank is 4 feet * 5 feet * 4 feet = 80 cubic feet.

(a) To empty half of the tank, we need to pump out 80/2 = 40 cubic feet of water.

The weight of the water being pumped out is 40 cubic feet * 62.4 pounds/cubic foot = 2528 pounds.

To pump the water out over the top edge, work has to be done against gravity, which means the work done is equal to the weight of the water times the height it's lifted, which is 4 feet.

Therefore, the work done in pumping half of the water out is 2528 pounds * 4 feet = 10112 foot-pounds.

(b) To empty the tank, we need to pump out 80 cubic feet of water.

The weight of the water being pumped out is 80 cubic feet * 62.4 pounds/cubic foot = 5056 pounds.

To pump the water out over the top edge, work has to be done against gravity, which means the work done is equal to the weight of the water times the height it's lifted, which is 4 feet.

Therefore, the work done in pumping all of the water out is 5056 pounds * 4 feet = 20224 foot-pounds.

The complete question is:-

A rectangular tank with a base of 4 feet by 5 feet and a height of 4 feet is full of water. The water weighs 62.4 pounds per cubic foot. How much work is done in pumping water out over the top edge in order to empty (a) half of the tank and (b) all of the tank?

To learn more about a rectangular tank, refer:-

https://brainly.com/question/27840674

#SPJ4

Another valid range value for this set of scores is 8, which is the interquartile range.

The range is a measure of the spread or variability of a dataset, and it is calculated as the difference between the largest and smallest values in the set. To find the range for the given set of scores, we first need to order the numbers from smallest to largest:

4, 6, 9, 11, 12, 14, 17

The smallest value in the set is 4, and the largest value is 17, so the range is:

17 - 4 = 13

Therefore, the range for the given set of scores is 13.

The range is a useful measure of variability that is simple to calculate and easy to interpret. However, it has a limitation in that it is sensitive to extreme values or outliers in the dataset. As a result, it may not always provide an accurate representation of the spread of the data.

Another measure of range that works particularly well for variables with precisely defined upper and lower bounds is the interquartile range (IQR). The IQR is calculated as the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of the dataset. It is commonly used with measurements of continuous variables and is less sensitive to extreme values than the range.

To calculate the IQR, we first need to find the median of the dataset. The median is the middle value when the numbers are arranged in order:

4, 6, 9, 11, 12, 14, 17

The median is 11.

Next, we need to find the first and third quartiles. The first quartile (Q1) is the median of the lower half of the dataset, and the third quartile (Q3) is the median of the upper half of the dataset. To find Q1 and Q3, we split the dataset into two halves:

Lower half: 4, 6, 9, 11

Upper half: 12, 14, 17

The median of the lower half is:

(6 + 9) / 2 = 7.5

The median of the upper half is:

(14 + 17) / 2 = 15.5

Therefore, the first quartile (Q1) is 7.5 and the third quartile (Q3) is 15.5.

The interquartile range (IQR) is the difference between Q3 and Q1:

IQR = Q3 - Q1 = 15.5 - 7.5 = 8

Therefore, another valid range value for this set of scores is 8, which is the interquartile range.

For more such questions on interquartile range.

https://brainly.com/question/15608154

#SPJ4

Given that the person is colorblind, the likelihood that they are male is around 0.926, or 92.6%.

As per the question given,  

Let's use Bayes' theorem to solve this problem.

Let M be the event that the person is male, and C be the event that the person is color-blind. We want to find the probability P(M|C), which is the probability that the person is male given that they are color-blind.

Using Bayes' theorem, we have:

P(M|C) = P(C|M) * P(M) / P(C)

We know that P(M) = 0.5, since 50% of the population are men. We also know that P(C|M) = 0.05, since 5% of men are color-blind. To find P(C), we can use the law of total probability:

P(C) = P(C|M) * P(M) + P(C|F) * P(F)

where F is the event that the person is female. We know that P(F) = 0.5, since 50% of the population are women, and we also know that P(C|F) = 0.004, since 0.4% of women are color-blind.

Substituting the values into Bayes' theorem, we have:

P(M|C) = 0.05 * 0.5 / (0.05 * 0.5 + 0.004 * 0.5)

= 0.926

Therefore, the probability that the person is male given that they are color-blind is approximately 0.926, or 92.6%.

For such more questions on Color blindness

https://brainly.com/question/13798882

#SPJ4

The best description for Newton's third law is: When a passenger stepped from a boat to the shore, the boat moved away from the shore.

Newton's third law of motion states that "For every action, there is an equal and opposite reaction". In other words, if an object A exerts a force on object B, then object B will exert an equal and opposite force back on object A. This is the underlying principle behind the concept of action-reaction pairs.

For example, if you push a wall, the wall will push back on you with an equal force, but in the opposite direction. The law applies to all types of forces, including gravitational, electromagnetic, and strong and weak nuclear forces.

It's important to note that the third law only applies to interactions between two objects. If a third object is involved, the forces will not necessarily be equal and opposite.

Read more on Newton's third law here:https://brainly.com/question/25998091

#SPJ1